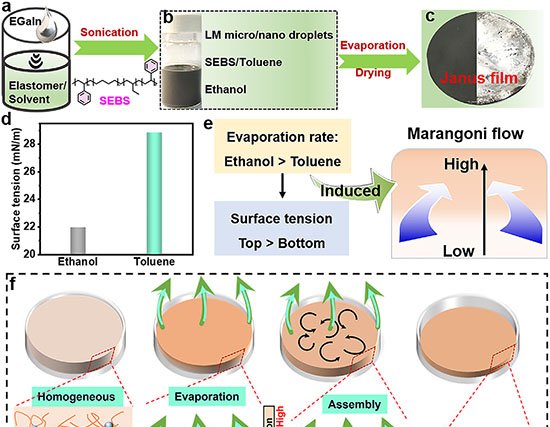
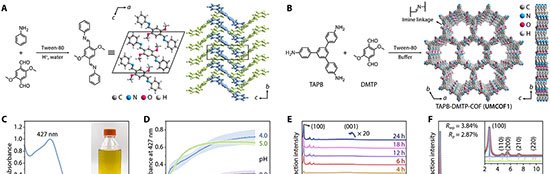
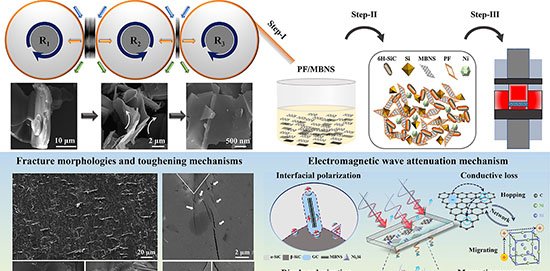
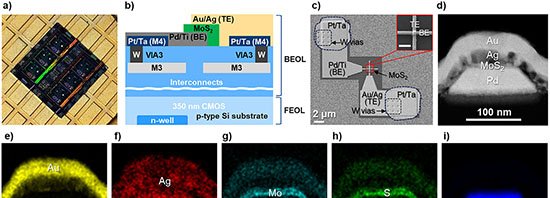
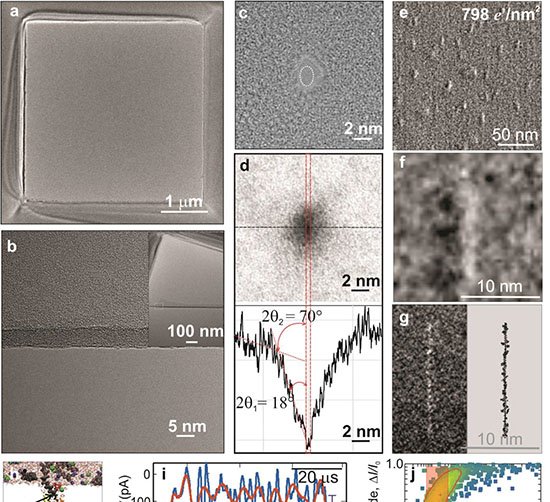
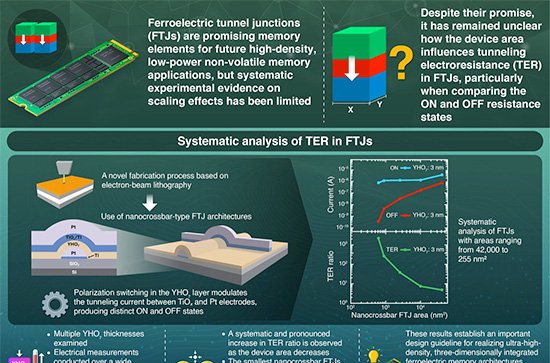
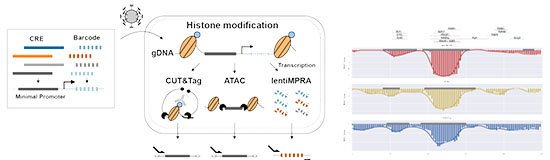
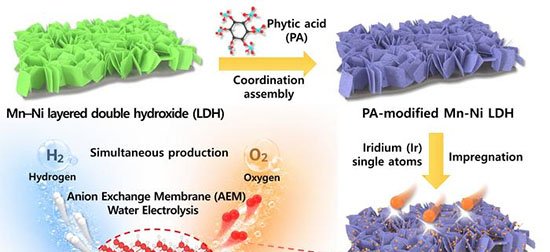
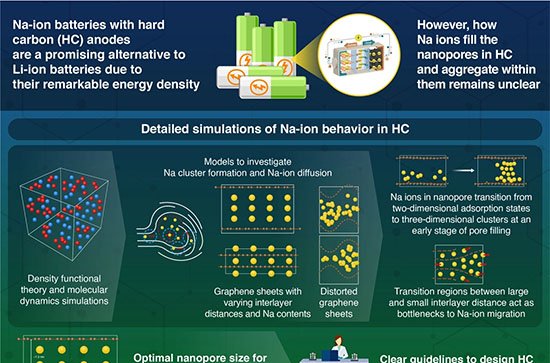
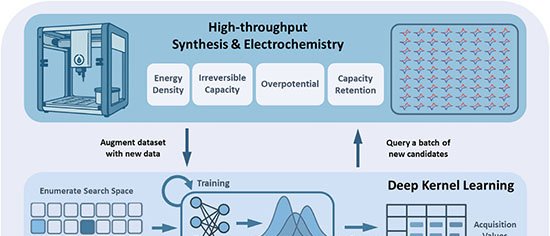
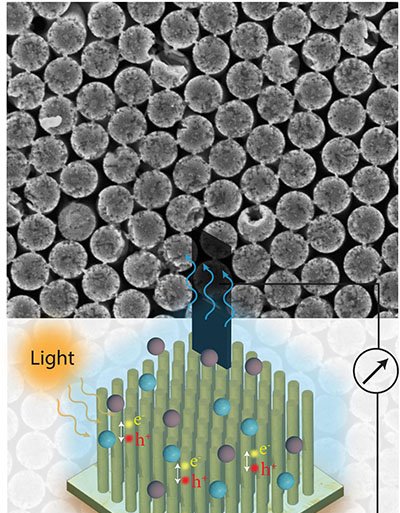
Uma equipe do Institute of Science Tokyo, em parceria com a Universidade de Tohoku, apresentou a primeira demonstração matemática de que a reentrância implica a existência de caos de temperatura em vidros de spin. O resultado, publicado em 27 de outubro de 2025 na revista Physical Review E, amplia a compreensão dos sistemas desordenados e pode beneficiar pesquisas em aprendizado de máquina e tecnologias quânticas.
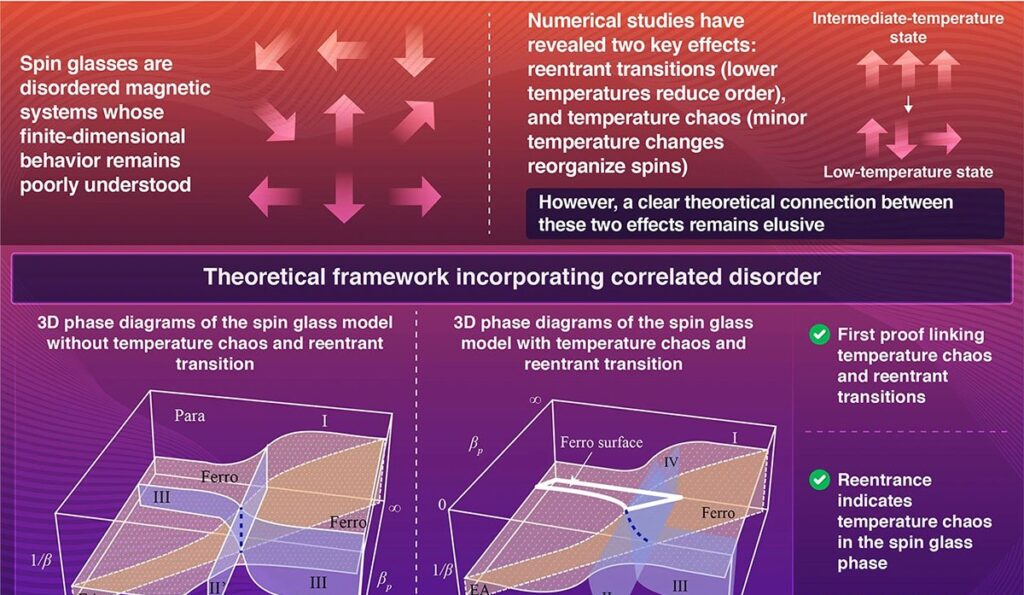
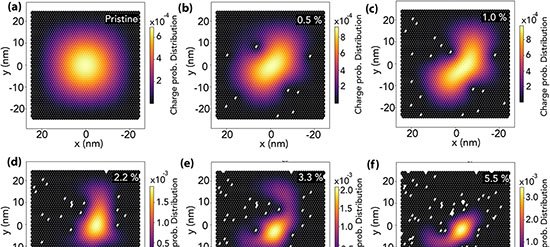
Vidros de spin são materiais magnéticos cujos spins atômicos orientam-se aleatoriamente, permanecendo “congelados” por longos períodos. Para descrever esse comportamento, físicos recorrem ao modelo de Edwards-Anderson (EA), que simula interações em duas e três dimensões. Dois fenômenos intrigantes emergem nesse modelo: a reentrância, em que o resfriamento reduz a ordem do sistema, e o caos de temperatura, no qual pequenas variações térmicas reorganizam completamente a configuração dos spins.
Como a relação foi demonstrada
Liderados pelo professor Hidetoshi Nishimori, os pesquisadores expandiram o modelo EA introduzindo correlações na desordem a fim de controlar o grau de frustração do sistema. A análise mostrou que, na ausência de caos de temperatura, a fronteira entre as fases ferromagnética e vidro de spin permanece linear. Quando essa linha se curva — fenômeno caracterizado como reentrante — o caos de temperatura surge inevitavelmente.
Segundo o grupo, o vínculo entre os dois efeitos foi provado com uma abordagem baseada em simetrias de gauge, sem recorrer a cálculos excessivamente complexos. A descoberta revela que comportamentos aparentemente imprevisíveis dos vidros de spin derivam de estruturas de simetria específicas e de correlações na desordem.
Implicações adicionais
O estudo também indica que, assumindo quebra de simetria de réplica no modelo EA, a distribuição de magnetização coincide com a distribuição de sobreposição de réplicas na chamada linha de Nishimori. Esse resultado desafia a visão predominante de que não haveria quebra de simetria de réplica nessa linha, conceito fundamental em inferência bayesiana e em algoritmos de aprendizado de máquina.

Imagem: Internet
Para Nishimori, o trabalho abre caminho para explicar como comportamentos complexos surgem em sistemas desordenados, tema relevante para materiais avançados, otimização computacional e correção de erros em computadores quânticos.
Com informações de Nanowerk